Situation :
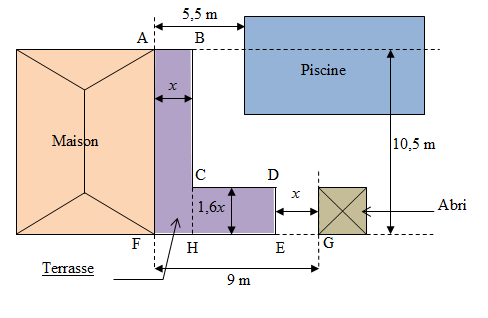
M. et Mme Materace souhaitent réaliser sur leur propriété une terrasse ABCDEF suivant le croquis ci-dessus.
Afin que l’ensemble reste harmonieux et que la terrasse réponde à leurs besoins, ils exigent du constructeur que les largeurs des deux « ailes » de cette terrasse aient les proportions suivantes : AB = x et ED = 1,6x.
L’aire de la surface de la terrasse A, en m², est alors donnée par :
A(x) = -3,2x² + 24,9x où x est la largeur AB de la terrasse
Problématique :
Quelles sont les dimensions de la terrasse afin que l’aire de la surface de la terrasse soit maximale ?
Capacités :
- Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction
- Étudier, sur un intervalle donné, les variations d’une fonction à partir du calcul et de l’étude de la dérivée. Dresser son tableau de variation
- Déterminer un extremum d’une fonction sur un intervalle donné à partir de son sens de variation
Connaissances :
- Fonction dérivée d’une fonction dérivable sur un intervalle I.
- Fonctions dérivées des fonctions de référence
- Notation f ‘(x).
- Dérivée du produit d’une fonction par une constante, de la somme de deux fonctions
- Théorème liant, sur un intervalle, le signe de la dérivée d’une fonction au sens de variation de cette fonction.






Aucun commentaire